Inference for Intractable Models

The problem

Researchers in Statistics and Machine Learning are having to work with ever-larger models developed by scientists or engineers. One particular challenge is that these models become so complex that standard tools for parameter estimation are not fit for purpose anymore. For example, most standard methods such as maximum likelihood estimation or Bayesian inference rely on the availability of a likelihood function that represents our model. But when the underlying phenomena being modelled is highly complex, it is often not possible to specify the likelihood associated to our model.

The term intractable model is a general term encompassing all models for which the corresponding likelihood function is not available. However, there are many different types of intractability. A first example includes intractable generative models or simulator-based models, which are models for which nothing is known about the likelihood function, but it is possible to simulate new data given a fixed value of the parameters. A second example are unnormalised models, in which case the likelihood function can be evaluated, but only up to some unknown normalisation constant. For each class of intractable model, alternative approaches need to be developed for parameter estimation.

Contributions to this field

My work in this area focuses on developing novel methodology for inference with intractable models which have several desirable properties. First, our algorithms should be robust in the sense that mild model misspecification or a few outliers should not have a disproportionate impact. This is particularly important when modelling complex phenomena because our models will ever be at best some reasonable idealisation of the underlying process. Second, the algorithm should be efficient in the sense that we obtain estimates which are as accurate as possible given the finite amount of data available. This is particularly important because collecting new data can be a costly process. Finally, the algorithms should be scalable and computationally efficient in the sense that they should be easy to implement and able to deal with large datasets or high-dimensional problems.

For simulator-based models, I have proposed and analysed novel estimators based on a family of distances called maximum mean discrepancy where specific instances can be chosen to balance the three desirable properties mentioned above:

• Briol, F-X., Barp, A., Duncan, A. B., Girolami, M. (2019). Statistical inference for generative models with maximum mean discrepancy. arXiv:1906.05944. (Preprint) (Talk/Video)

• Key, O., Fernandez, T., Gretton, A. & Briol, F-X. (2021). Composite goodness-of-fit tests with kernels. arXiv.2111.10275. (Preprint) (Code)
  • A preliminary version of the paper was accepted to the NeurIPS 2021 workshop “Your Model is Wrong: Robustness and misspecification in probabilistic modeling”.

• Dellaporta, C., Knoblauch, J., Damoulas, T. Briol. F-X. (2022). Robust Bayesian inference for simulator-based models via the MMD posterior bootstrap. Proceedings of The 25th International Conference on Artificial Intelligence and Statistics (AISTATS), PMLR 151:943-970. (Conference) (Preprint) (Code) (Video)

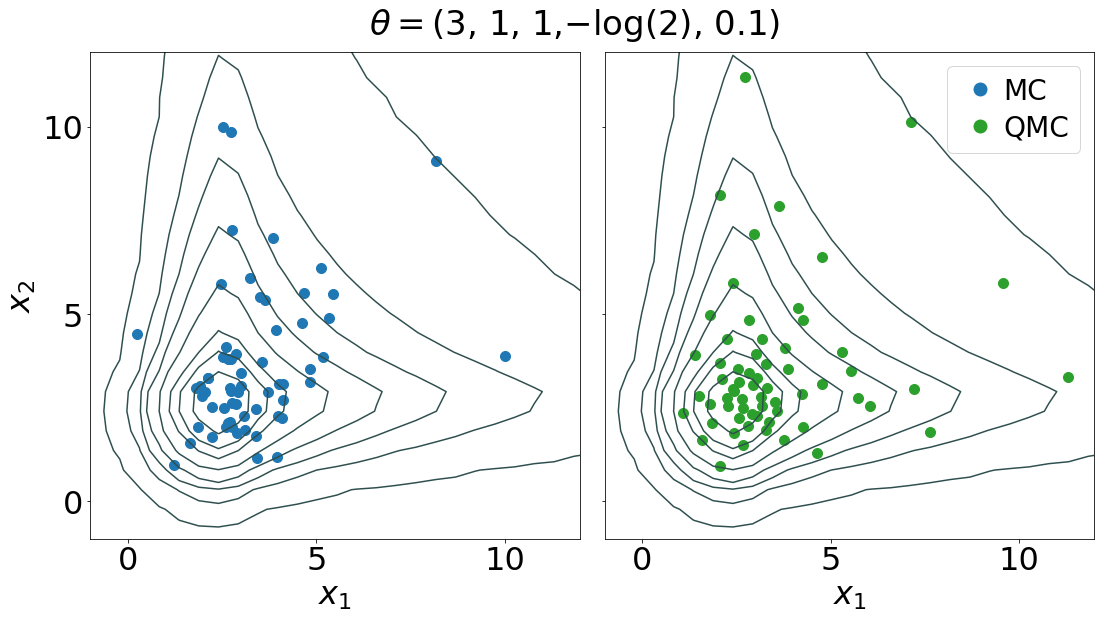
• Niu, Z., Meier, J. & Briol, F-X. (2023). Discrepancy-based inference for intractable generative models using quasi-Monte Carlo. Electronic Journal of Statistics, 17 (1), 1411-1456. (Journal) (Preprint) (Code)

• Bharti, A., Naslidnyk, M., Key, O., Kaski, S., & Briol, F-X. (2023). Optimally-weighted estimators of the maximum mean discrepancy for likelihood-free inference. Proceedings of the 40th International Conference on Machine Learning, PMLR 202:2289-2312. (Conference) (Preprint) (Code)

• Bharti, A., Huang, D., Kaski, S. & Briol, F-X. (2024). Cost-aware simulation-based inference. arXiv:2410.07930. (Preprint) (Code)

For unnormalised models, a convenient choice of distance are the so-called Stein discrepancies, which I have used to obtain flexible families of frequentist statistical estimators or generalised Bayesian inference approaches.

• Barp, A., Briol, F-X., Duncan, A. B., Girolami, M., Mackey, L. (2019). Minimum Stein discrepancy estimators. Neural Information Processing Systems, 12964-12976. (Conference) (Preprint) (Talk/Video)

• Mastubara, T., Knoblauch, J., Briol, F-X. & Oates, C. J. (2022). Robust generalised Bayesian inference for intractable likelihoods. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 84:3, 997– 1022. (Journal) (Preprint) (Code) (Video)
  • This paper received a Student Paper Award from the section on Bayesian Statistical Science of the American Statistical Association in 2022.
  • This paper received a Best Student/Postdoc Contributed Paper Award at ISBA 2021.
  • A preliminary version of the paper was accepted to the NeurIPS 2021 workshop “Your Model is Wrong: Robustness and misspecification in probabilistic modeling”.
• Matsubara, T., Knoblauch, J., Briol, F-X. & Oates, C. J. (2023). Generalised Bayesian inference for discrete intractable likelihood. arXiv:2206.08420. Accepted (subject to minor revisions) at the Journal of the American Statistical Association. (Journal) (Preprint) (Code)

As part of my work in the Data-Centric Engineering programme of The Alan Turing Institute, I have also worked in specialising some of the methods above to solve important engineering problems, in particular in the field of telecommunications:

• Bharti, A., Briol, F-X., Pedersen, T. (2022). A general method for calibrating stochastic radio channel models with kernels. IEEE Transactions on Antennas and Propagation, vol. 70, no. 6, pp. 3986-4001, June 2022. (Journal) (Preprint) (Code)
  • A preliminary version of this paper was accepted to the NeurIPS 2021 workshop on Machine Learning and the Physical Sciences.
• Briol, F-X., Bharti, A. (2021). Using machine learning to improve the reliability of wireless communication systems. (Turing Institute Blog Post)