Stein’s Method as a Computational Tool

About

My main research interests consist in developing novel statistical or machine learning methodology which can deal with computational expensive or intractable models. From a computational viewpoint, two of the main challenges in this context are:

• We usually want to obtain certain quantities of interest, but these take the form of some intractable integrals/expectations. Examples include Bayesian posterior moments, marginal likelihoods, expected losses or distances on probability distributions.

• We often know probability density functions only up to some unknown normalisation constant. For example, the normalisation constant of Bayesian posterior distributions (called the model evidence) is often intractable, and sometimes the likelihood itself has an unknown constant (this is sometimes called an unnormalised model, or a doubly-intractable problem in Bayesian settings).

A common approach for tackling these problems is to use elaborate Monte Carlo methods or variational inference, but this can often lead to significant further computational challenges. Thankfully, Stein’s method offers us an alternative approach.

Using so-called Stein operators, it is straightforward to construct functions which integrate to a known constant value, and which can be evaluated even without knowing normalisation constants of the densities of interest. The approach is particularly powerful because this can be done with minimal assumptions on the distribution we are integrating against. For example, suppose you are performing some Bayesian analysis and have a corresponding posterior distribution. Then, Stein operators can give you a large family of functions whose expectation under this posterior are known.

Why is this useful? Well with a bit of work and the design of novel methodologies and algorithms, all of the intractable integrals/expectations mentioned above can usually be replaced by integrals with a known value. This can for example be used to construct notions of distance between probability distributions called Stein discrepancies.

Contributions to this field

I have developed novel methodology in a range of fields using Stein’s method. In particular, I have focused on developing novel tools for Monte Carlo methods, and novel statistical estimators in frequentist and Bayesian settings. Before diving into these, you might like to get an in-depth introduction to this topic. One approach to this is the following review paper:

• Anastasiou, A., Barp, A., Briol, F-X., Ebner, B., Gaunt, R. E., Ghaderinezhad, F., Gorham, J., Gretton, A., Ley, C., Liu, Q., Mackey, L., Oates, C. J., Reinert, G. & Swan, Y. (2023). Stein’s method meets Computational Statistics: A review of some recent developments. Statistical Science, Vol. 38, No. 1, 120-139. (Journal) (Preprint 1) (Preprint 2)

If you already know about Stein’s method, you might instead be interested in my work in a range of areas including:

• Control variates to reduce the variance of Monte Carlo/MCMC estimators:

  • Oates, C. J., Cockayne, J., Briol, F-X. & Girolami, M. (2019). Convergence rates for a class of estimators based on Stein’s identity. Bernoulli, Vol. 25, No. 2, 1141-1159. (Journal) (Preprint)

  • Si, S., Oates, C. J., Duncan, A. B., Carin, L. & Briol. F-X. (2021). Scalable control variates for Monte Carlo methods via stochastic optimization. Accepted for publication in the proceedings of the 14th Monte Carlo and Quasi-Monte Carlo Methods (MCQMC) conference 2020. arXiv:2006.07487. (Conference) (Preprint) (Video)

• Sun, Z., Barp, A. & Briol, F-X. (2023). Vector-valued control variates. Proceedings of the 40th International Conference on Machine Learning, PMLR 202:32819-32846. (Conference) (Preprint) (Code)
  • This paper received a Student Paper Award from the section on Bayesian Statistical Science of the American Statistical Association in 2022.
  • Zhuo Sun was awarded a Silver Medal for his poster on this paper at the 2021 Fry conference at Bristol.
• Sun, Z., Oates, C. J. & Briol, F-X. (2023). Meta-learning control variates: variance reduction with limited data. Proceedings of the Thirty-Ninth Conference on Uncertainty in Artificial Intelligence, PMLR 216:2047-2057. (Conference) (Preprint) (Code)
  • This paper was accepted for oral presentation at UAI.

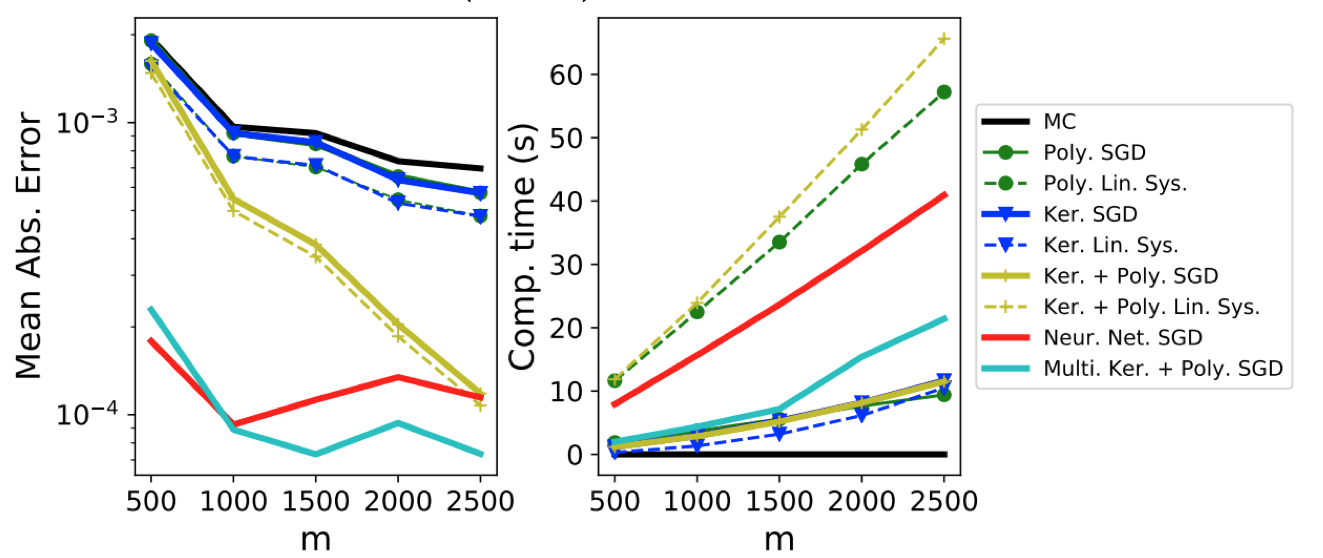
• Statistical estimation methods for models with unnormalised likelihoods:

  • Barp, A., Briol, F-X., Duncan, A. B., Girolami, M., Mackey, L. (2019). Minimum Stein discrepancy estimators. Neural Information Processing Systems, 12964-12976. (Conference) (Preprint) (Talk/Video)
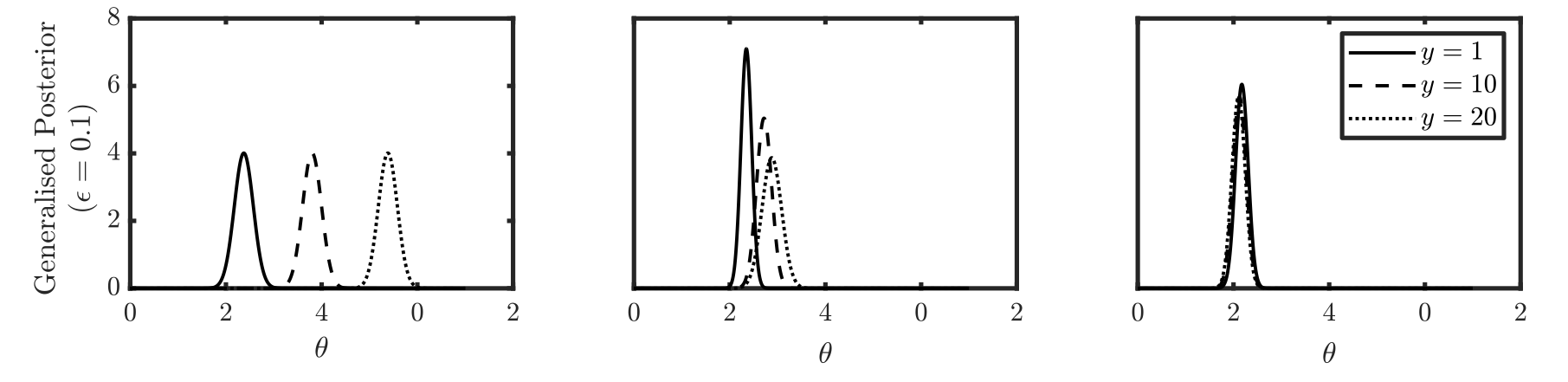
  • Mastubara, T., Knoblauch, J., Briol, F-X. & Oates, C. J. (2022). Robust generalised Bayesian inference for intractable likelihoods. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 997– 1022. (Journal) (Preprint) (Code) (Video)
    • This paper received a Student Paper Award from the section on Bayesian Statistical Science of the American Statistical Association in 2022.
    • This paper received a Best Student/Postdoc Contributed Paper Award at ISBA 2021.
    • A preliminary version of the paper was accepted to the NeurIPS 2021 workshop “Your Model is Wrong: Robustness and misspecification in probabilistic modeling”.

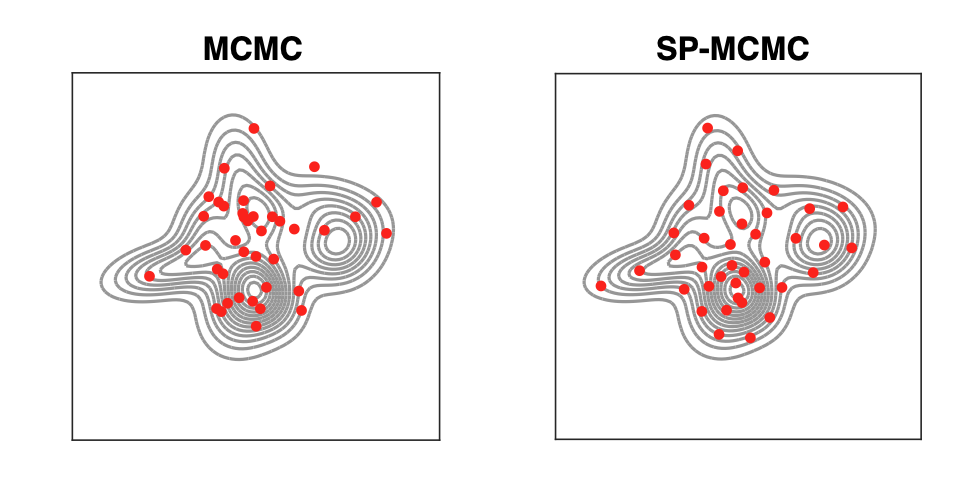
• Novel samplers for approximating complicated probability distributions such as Bayesian posterior distributions:

  • Chen, W. Y., Mackey, L., Gorham, J. Briol, F-X. & Oates, C. J. (2018). Stein points. International Conference on Machine Learning, PMLR 80:843-852. (Conference) (Preprint) (Code)

  • Chen, W. Y., Barp, A., Briol, F-X., Gorham, J., Girolami, M., Mackey, L., Oates, C. J. (2019). Stein point Markov chain Monte Carlo. International Conference on Machine Learning, PMLR 97:1011-1021. (Conference) (Preprint) (Code)