Bayesian Robustness
The problem
In statistics and machine learning, we typically develop probabilistic models which represent real-world phenomena. These models are at best mathematical idealisations and are therefore limited by our understanding of the world. They will also inevitably contain approximations such as omitted variables, incorrect functional forms, or incorrect distributional assumptions. This is a particular concern in safety critical applications, such as medical diagnosis, self-driving cars, or the criminal justice system, where model misspecification can have a severe impact. As a result, it is necessary to develop robust methods which can perform reasonably well when models are mildly misspecified.
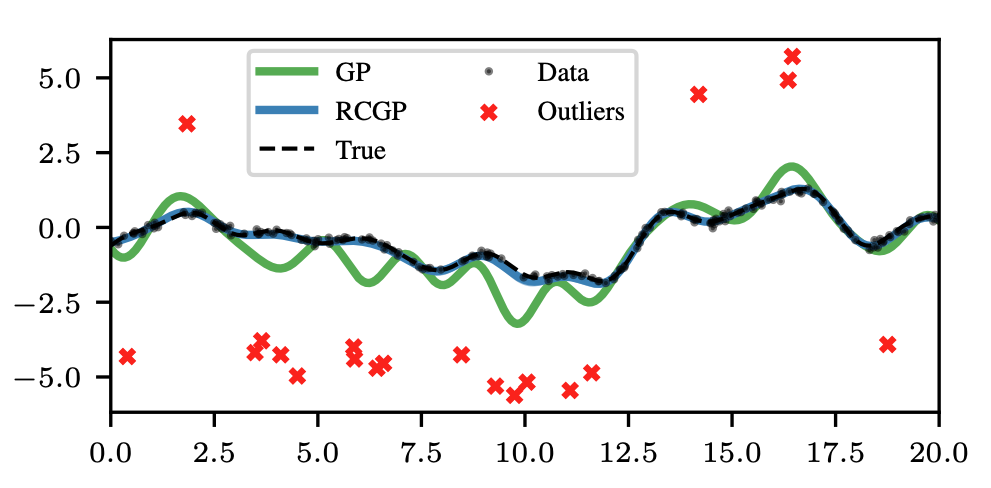
Robustness is particularly important in Bayesian inference, since we would ultimately like to use Bayesian posterior distributions to represent our uncertainty about quantities of interest. But if the model is misspecified, not only will Bayesian methods return poor predictions, their posterior uncertainty will also become meaningless. The issue of poor predictions is illustrated in the figure below in the case of Gaussian processes (GPs); due to a small proportion of outliers, the posterior mean of a standard GP is significantly biased, and we would ideally prefer the robust alternative (RCGP) which provides much more accurate predictions of the truth.
Contributions to this field
My contributions to this field have been on the development of novel Bayesian methods which are robust to mild misspecification. The main tool I have used is generalised Bayesian inference, which allows for updates from a prior distribution without necessarily being significantly impacted when the likelihood function is misspecified.
One line of work has been on designing robust Bayesian methods for “intractable likelihood” models. In this case, we need updates which are both robust but also computationally feasible without direct access to evaluations of the likelihood:
- Dellaporta, C., Knoblauch, J., Damoulas, T. Briol. F-X. (2022). Robust Bayesian inference for simulator-based models via the MMD posterior bootstrap. Proceedings of The 25th International Conference on Artificial Intelligence and Statistics (AISTATS), PMLR 151:943-970. (Conference) (Preprint) (Code) (Video)
- This paper received the Best Paper Award at AISTATS 2022 (out of 1685 submissions and 492 accepted papers).
- A preliminary version of the paper was accepted to the NeurIPS 2021 workshop “Your Model is Wrong: Robustness and misspecification in probabilistic modeling”.
- This paper was discussed on the blog of Prof. Christian Robert
- Matsubara, T., Knoblauch, J., Briol, F-X. & Oates, C. J. (2022). Robust generalised Bayesian inference for intractable likelihoods. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 84:3, 997– 1022. (Journal) (Preprint) (Code) (Video)
- This paper received a Student Paper Award from the section on Bayesian Statistical Science of the American Statistical Association in 2022.
- This paper received a Best Student/Postdoc Contributed Paper Award at ISBA 2021.
- A preliminary version of the paper was accepted to the NeurIPS 2021 workshop “Your Model is Wrong: Robustness and misspecification in probabilistic modeling”.
- Matsubara, T., Knoblauch, J., Briol, F-X. & Oates, C. J. (2024). Generalised Bayesian inference for discrete intractable likelihood. Journal of the American Statistical Association (to appear). (Journal) (Preprint) (Code)
Another line of work has been on taking existing Bayesian models and making them robust. There are many existing approaches to this, typically by modifying the likelihood, but this tends to break any computational advantages of these methods such as conjugacy. My work has therefore focused on developing Bayesian methods which are both robust and scalable. Examples includes Gaussian process regression, Kalman filtering, and online changepoint detection:
Altamirano, M., Briol, F-X. & Knoblauch, J. (2023). Robust and scalable Bayesian online changepoint detection. Proceedings of the 40th International Conference on Machine Learning, PMLR 202:642-663. (Conference) (Preprint) (Code) (Video)
- Altamirano, M., Briol, F-X. & Knoblauch, J. (2024). Robust and conjugate Gaussian process regression. Proceedings of the 41st International Conference on Machine Learning, PMLR 235:1155-1185. (Conference) (Preprint) (Code)
- This paper was accepted as a spotlight paper (top 3.5% of submitted papers).
- Duran-Martin, G., Altamirano, M., Shestopaloff, A. Y., Sanchez-Betancourt, L., Knoblauch, J., Jones, M., Briol, F-X. & Murphy, K. (2024). Outlier-robust Kalman filtering through generalised Bayes. Proceedings of the 41st International Conference on Machine Learning, PMLR 235:12138-12171. (Conference) (Preprint) (Code)
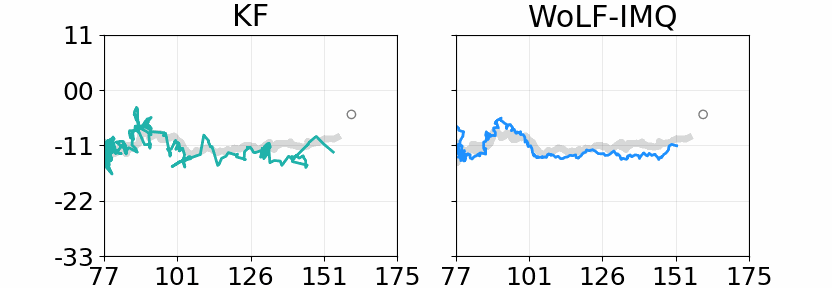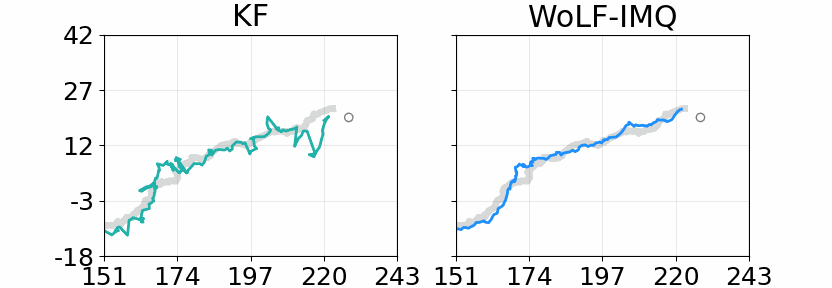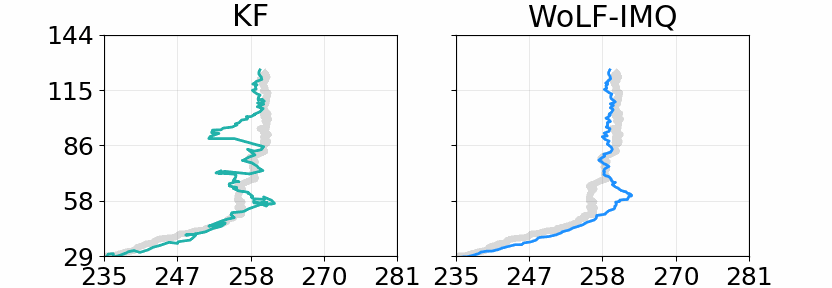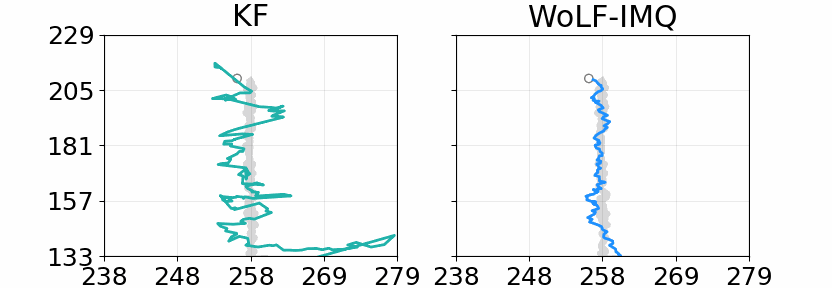
- Laplante, W., Altamirano, M., Duncan, A., Knoblauch, J. & Briol, F-X. (2025). Robust and conjugate spatio-temporal Gaussian processes. arXiv:2502.02450. To appear at ICML 2025. (Conference) (Preprint) (Code)
Beyond Bayesian methods, I have also been developing hypothesis testing methods, which are either able to detect model misspecification, or be robust to it. Although I have not specifically applied these to Bayesian inference, they very much could be used for this problem too.
Liu, X. & Briol, F-X. (2024). On the robustness of kernel goodness-of-fit tests. arXiv:2408.05854. (Preprint) (Code)
Key, O., Gretton, A., Briol, F-X. & Fernandez, T. (2025). Composite goodness-of-fit tests with kernels. Journal of Machine Learning Research, 26(51):1−60, 2025. (Journal) (Preprint) (Code) (Video)
- A preliminary version of the paper was accepted to the NeurIPS 2021 workshop “Your Model is Wrong: Robustness and misspecification in probabilistic modeling”.
Funding
- EPSRC Small Grant in the Mathematical Sciences grant (EP/Y011805/1) on “Robust Foundations for Bayesian Inference”.
